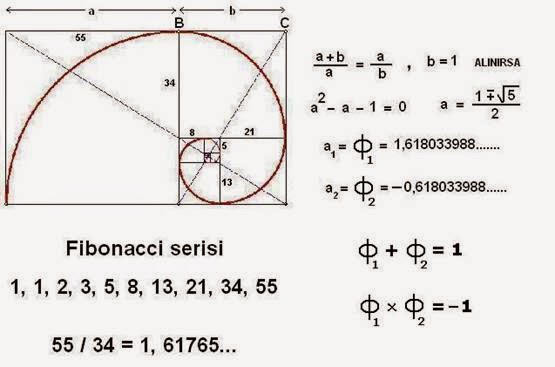
İtalyan matematikçi Fibonacci,1202 yılında matematik, doğa ve sanat arasındaki bir bağı gözler önüne serdi.
1202 yılında, İtalyan matematikçi - Pisa’lı Leonardo, ya da bilinen adıyla Fibonacci, matematik, doğa ve sanat arasındaki bir bağı gözler önüne serdi. Fibonacci, sadece Hıristiyan dünyasına, Hindu-Arap dünyasında günümüzde de kullanılan rakamları tanıtmadı, tavşanlarla ilgili -derin etki yaratacak- bir problemi de ortaya attı. Fibonacci, bir çift tavşandan yılda kaç tavşan türeyeceğini bilmek istedi. Ocak ayından başlayarak, her ay her bir çiftin bir aylık olduğunda yeni bir çift doğuracağını varsaydı. Çözüm üzerinde çalıştıkça ilginç bir tabloyu - kalıbı fark etti: tavşan sayısı her ay kesin bir mantık sisteminde artmaktaydı. 1, 2, 3, 5, 8, 13, 21 gibi. Serideki her sayı kendinden önce gelen son 2 sayının toplamına eşitti. 1 + 2 =3, 3 + 5 = 8, 5 + 8 = 13 gibi…
Sonsuza dek giden bu sayılar ‘Fibonacci Serisi’ olarak bilinir. Bu, küçük bir tesadüf gibi görülebilir ancak bu sayılar sürülerce tavşandan çok daha gizemli kapıları açacak bir anahtar gibidir. Örneğin, botanikte çiçeklerin yapıları, Fibonacci sayılarına dayanmakta. Zambakların 3’e dayalı bir radyal simetrisi vardır. Menekşenin 5; ayçiçeğin toplamda 33, 55 ya da 89 yaprağı vardır.
Genetiğin ötesinde gelişmenin doğal dinamiğine ilişkin gibi gözüken bu olgu, 1993 yılına dek açıklanamadı. Bunun da ötesinde, ayçiçeğin ardışık çekirdeklerinin dizilişindeki sarmal, çemberli deniz kabuğunun yapısındaki spiral veya akciğerlerdeki bronşçukların çatallaşan yapılanması; bunların hepsinde organik büyüme çoğu kez Fibonacci serisinden çıkarılan matematiksel orantıya uyar.
Altın Oran
Fibonacci sayıları büyüdükçe, serideki herhangi 2 ardışık sayının birbirine oranı, 1,618 ile başlayan devirli bir ondalık sayıya yaklaşır, ancak bu sayıya ulaşamaz. Bu orana ‘Kutsal Orantı’ adı verildi. Kısa bir süre sonra da ‘Altın Oran’ dendi. Sonunda, (Yunanistan’daki Athena’nın tapınağı olan) Parthenon tapınağındaki tasarımın mimarı olan Yunan heykeltıraşların öncüsü Phidias’ın ismine ithafen isminin kısaltması olarak ‘Fi’ adı verildi.
M.Ö 500’lerdeki ilk Pythagorean okulundan beri Yunanlılar ‘Fi’ oranı üzerinde çalışmalar yaptılar ve kenarları 1 ve ‘Fi’ye eşit bir dikdörtgen yapma yöntemini geliştirdiler. Bir karenin tam ortasından yana doğru bir ark çizip altını tamamladıklarında, sonradan ‘Altın Dikdörtgen’ diye anılan dikdörtgeni yaptılar. Ayrıca, bu şekilden kareyi çıkardıklarında, geriye kalanın yine bir ‘Altın Dikdörtgen’ olduğunu fark ettiler.
Yunanlılar ‘Altın Dikdörtgen’nin, matematiksel güzelliğin anahtarını barındırdığına inandılar ve onu birçok tasarıma dâhil ettiler. Bunun en çarpıcı örneği belki de simetrisinin çoğu ‘Altın Dikdörtgen’e uyan Parthenon tapınağıdır. Mimarilerinde ‘Fi’nin görsel uyumunu ilk kullananlar Yunanlılar değildi. 5000 yıl önce Mısırlılar büyük Keops piramidinin tasarımını da Altın Oranlara dayandırmışlardı. Bu ölçümleme dikkat çekmemiş olabilir, ancak ‘Fi’nin evrensel bir estetik dayanak olduğuna dair kanıyı güçlendirmektedir.
Asırlarca biyologlar doğanın karmaşası ile didişirken sanatçılar da güzelliğin psikolojisi üzerinde çalıştılar. Sonunda 800 küsur yıl önce bu 3 bilim dalını (matematik, doğa ve sanat) birleştiren ve daha derin bir kavramayı sağlayan bağı bulan, İtalyan matematikçi Fibonacci oldu.
Altın Oran’ı sanatta ve mimaride oldukça fazla görmekteyiz. Aynı zamanda resimde, müzik notlarında, şiir, ekonomi gibi birçok alanda altın oran bulunmaktadır.

GÜNLÜK YAŞAMDA ALTIN ORAN
İnsanın İşaret Parmağı
Bir insanın işaret parmağının (normal standartlardaki parmaklar için geçerli) her bir bölümünün bir önceki bölüme oranı, Fibonacci sayısını veriyor.
Akciğerler
Akciğeri oluşturan bronş ağacının görülen en belirgin özelliği asimetrik olmasıdır. Soluk borusu, biri uzun (sol) ve diğeri de kısa (sağ) olmak üzere iki ana bronşa ayrılır. Kısa bronşun uzun bronşa olan oranının yaklaşık olarak 1/1,618 değerini verdiği saptanmıştır.
İnsan Yüzü
Kulaklar arasındaki mesafe, gözle üst dudak arasındaki, burnun altı ile çene arasındaki mesafe altın oran içermektedir.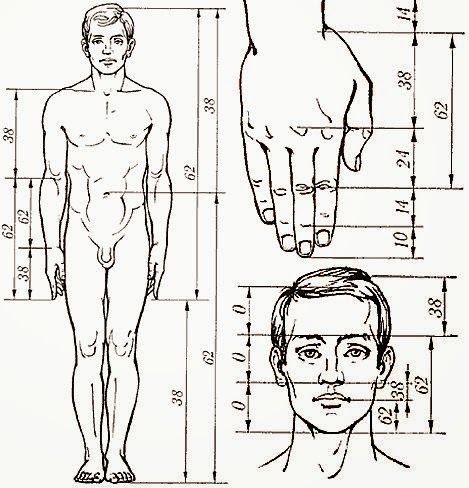
Kollar
Kolumuzun üst bölümünün alt bölüme oranı altın oranı verir.
Mısır Piramitleri
Her bir piramidin tabanının, yüksekliğine oranı altın oranı veriyor.
Çam Kozalağı
Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller oluşturarak çıkarlar. Eğrinin eğrilik açısı altın orandır.
Doğada Fibonacci sayısı
Bir bitkinin sapındaki yaprakların, bir ağacın dallarının düzeninde, her zaman altın oran kuralı vardır. Yapraklardan biri başlangıç noktası olarak alındığında, bundan başlayarak yukarıya ya da aşağıya doğru sayılırsa, farklı bitkiler için farklı sayılar bulunabilir ancak bunların tek ortak özellikleri Fibonacci sayıları olmalarıdır. Bir papatyanın yaprak sayılarının da 21, 34, 55, 89 yani Fibonacci sayılarını verdiği bilinir.
Kaynak
https://www.youtube.com/watch?v=QVmzntcoAPE
http://www.bilgiustam.com/fibonacci-sayilari-ve-altin-oran-nedir/